Форум PHP программистов > Взаимно простые числа.

[ Поиск ] - [ Пользователи ] - [ Календарь ]

Страницы: 1, 2

html-программист

19.08.2013 - 22:47

Паттерн

В 2002 году придумал интересную штуку. 14 лет тогда было. Размышлял о фракталах и теории хаоса, а учиться не хотел. Учиться не хотел, а в школу ходить заставляли. Придумал способ убить время на скучных уроках по истории, географии и прочей гуманитарии. Попробую объяснить подробно. Все, что нам нужно - листок в клетку и карандашик. Если листка в клетку нет в наличии и карандашик тоже отсутствует - онлайн версия на JavaScript http://xcont.com/pattern.html (в исходники не заглядывайте - тем говнокод:)

Алгоритм прост до неприличия. Собственно выглядит сие вот так:

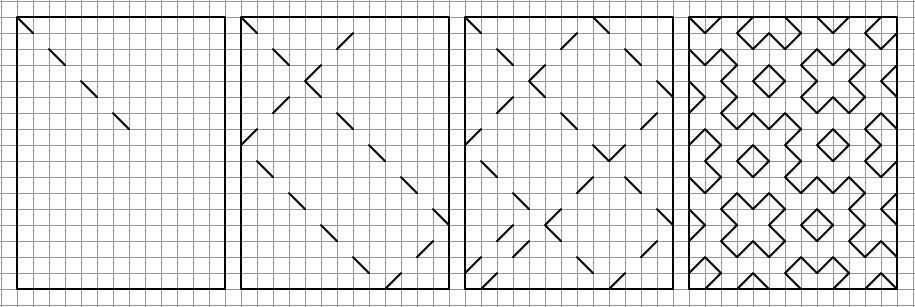
user posted image

Выделяем прямоугольную область и пускаем из угла "квантовый луч" (так я его называл в 2002 году - сильно за терминологию не ругайте). Луч отражается от стенок и пропадает в другом углу.

Если соблюдаются определенные условия (об этом дальше) - получается фрактальный (об этом тоже дальше) узор-паттерн.
Если условия не соблюдаются (очевидный например - стороны прямоугольника равны) - узор не получается. Из менее очевидных напримеров - узор так-же не получается, если размеры сторон имеют общий делитель. Фактически, узоры получаются только если размеры обоих сторон - взаимно простые числа (http://ru.wikipedia.org/wiki/Взаимно_простые_числа ).

Наглядно (и кликабельно):

кстати, все сделано вручную, по пикселям в Paint

На картинке все числа от 1 до 30.

А теперь немного о Фибоначчи и фракталах.

Все узоры представляют из себя фракталы.

От чего зависит узор?

Цитата

А потому, что нужно, чтобы разница тоже была простым числом (наиболее большим), его разница с числами тоже была простой и не маленькой, и т.д., тогда будет что-нибудь интересное.

Что наводит нас на мысль - а если попробовать числа Фибоначчи? Пацан сказал - пацан сделал.
http://ru.wikipedia.org/wiki/Числа_Фибоначчи

Закрашивал в Paint самые большие замкнутые области.

user posted image

233х144:

987х610 (скукожил в 5 раз):
user posted image

233х144 и 987х610 - идентичны

Фракталы, как они есть.

Что еще можно из этого сделать:

1. Попробовать не прямоугольную область, а скажем элипс.
2. Попробовать сделать в трех измерениях.
3. Обнаружить другие интересные зависимости между числами и рождаемым ими фракталом.

На хабре объяснил не подробно, о чем сейчас жалею. http://habrahabr.ru/sandbox/68846/ Есть интересная информация, чтобы дополнить статью, но дополнить не могу - ибо read-only. Поэтому буду выпрашивать инвайт, если кому не жалко (пазязя)

Засим откланяюсь и буду надеяться на вашу доброту (дайти инвайтик, пазязя). Инвайтик сюда: admin@xcont.com или сюда: serg530@i.com.ua

P.S.

И немножко шизофрении 11-ти летней давности:

Цитата

Тогда размышлял, о соотношениях хаоса и порядка, откуда в хаосе берется порядок, и в порядке - хаос. Так вот была тогда мысль, что когда все взорвалось (большой взрыв, в который я свято верил), был луч электромагнитной энергии который в начале бегал в маленьком пространстве (которое далее расширялось). Поскольку электромагнитные волны можно представить в виде квантов - этот луч не непрерывный. Там где мы видим пересечения электромагнитных волн - там появляется "материя" (http://ru.wikipedia.org/wiki/Рождение_пар) в виде фрактальных узорчиков. Так из хаоса рождается порядок.

(2) у пространства нет кванта расстояния - поэтому нет общих делителей. Всегда получается узор (то, что мы называем материей).
(1) вселенная расширяется непрерывно и плавно. Узорчик непрерывно (и тоже плавно) переходит из одного в другой - то, что мы называем движением материи.

Цитата

Ну и еще выводы:
1. Вселенная не двухмерная, а трехмерная (а с точки зрения Общей Теории Относительности - четырехмерная).
2. Опять-же, с точки зрения ОТО - вселенная - не прямоугольная. Топологически, вселенную можно представить в виде тора.
Поэтому узорчики на порядок сложнее.

Быстрый ответ:

Здесь расположена полная версия этой страницы.